你的耳朵一直在偷偷做傅里叶变换，你的脑子却学不会

每年，不知道有多少崭新出厂的大学生反复吊死在同一棵树上，这棵树就是高数。而傅立叶变换又是高等数学中最实用的内容之一。

用比较时髦的方式来说，如果说线性代数是“人工智能的数学基础”，那么傅立叶变换就是“机器视觉的数学基础”。傅立叶变换重要到，在高等数学之后的数学、物理、工程课程上，不少都需要以傅立叶变换为基础进行分析，教授往往会默认你已经学会了傅立叶变换。

但这么重要的傅立叶变换，在不少教材中，却往往以傅立叶级数的形式，隐藏在教材目录的末尾。只追求不挂科飘过的同学是学不到这里的，但它又十分重要。在以后的课程中，有些同学再接触到傅立叶变换时，才追悔莫及地去补课，但又啃不下来。如果你正面临这样的困难，我非常推荐你搜索3blue1brown的线性代数、微积分、傅立叶变换的视频。

但是，如果我告诉你，你苦苦学不会的傅立叶变换，你的耳朵时时刻刻都背着你在做，你会是什么感受？

频率终极解决方案

我们能分辨多彩缤纷的颜色，也能分清楚歌曲音调的高低，而颜色和音调高低，其实分别体现了可见光（电磁波）的频率和音波的频率。人眼如何分辨颜色，初中生物就学过——人眼视网膜上有三种不同的视锥细胞，它们对不同波长的光敏感，可以将这些信号转换成电信号传入大脑。而三种视锥细胞敏感的光，被我们称为三原色，分别是红色、绿色和蓝色。

那耳朵又是如何听到声音、分辨音调的？听到声音的过程初中生物也教过，就是声音从外而传导到鼓膜，鼓膜后面的中耳、内耳再把声音的振动转换成电信号传入大脑。

但后一个问题，耳朵又是如何分辨音调的？初中生物可能就无法给你比较直观的解答了。因为音调本质就是音波振动频率，声波的振动频率越高，声调也就越高、声音就越尖。视频在加速时，同一段声音波形的总时长减短，音调也就提升了，所以加速的视频音调听起来会是尖尖的，甚至还有点搞笑。

而要处理不同的频率，那就要请出频率终极解决方案——傅立叶变换了。

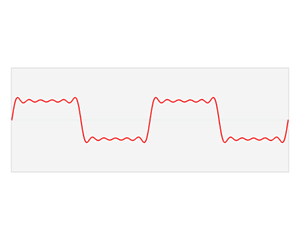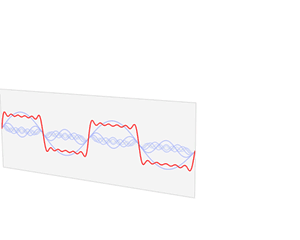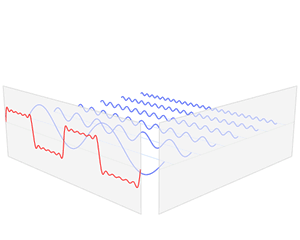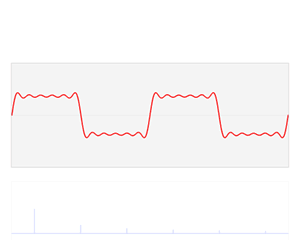
傅立叶变换可以将一段随时间变化的信号，转换成它在频率上分布的情况。也就是说，通过傅立叶变换，我们可以找出一段波动信号中，存在哪些频率的声波。而这些频率就对应着声音的音调。

当然，严格的傅立叶变换需要输入信号的时间是无限长，但实际哪会有时间无限长的信号？所以我们这里讨论的是傅立叶变换这个大类，里面可能包含短时傅立叶变换、离散傅立叶变换等。

等等，明明那么多人都学不会傅立叶变换，那耳朵是如何用傅立叶变换分辨频率的？实际上，耳朵中最关键的结构之一：耳蜗，它本质上是一个傅立叶分析装置。

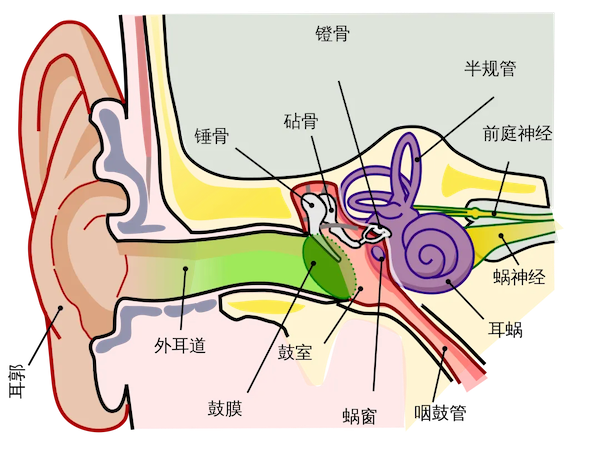
声音从耳道向内传播，鼓动了鼓膜，鼓膜的振动通过锤骨、砧骨、镫骨（人体内最小的三块骨头）传导到耳蜗。耳蜗是一个管状螺旋结构，里面充满液体，能增大音波的振动强度。

耳蜗管的半径随着螺旋改变，其中还有沿着耳蜗的基底膜（basilar membrane），耳蜗外缘的基底膜非常坚硬，耳蜗管也很薄，在耳蜗向内螺旋时，基底膜又会松弛，耳蜗管宽阔一些。就好像松紧程度不一样的琴弦具有不同的音调一样，基底膜机械性质不同，它们的固有频率也会不同，会对不同频率的声音震动更敏感。

基底膜上还有毛细胞（hair cell），基底膜的振动会刺激它产生神经信号，从而让我们听到声音。由于耳蜗和基底膜的螺旋机械结构，在耳蜗靠外的地方，对高频震荡比较敏感。随着耳蜗向内螺旋，固有频率也会越来越低。耳蜗和基底膜共同组成了一个天然的、机械的、被动的傅立叶分析装置，将音波振动频率分散到了耳蜗的各个位置。这样，不同位置的毛细胞传出的神经信号，就相当于不同的频率的声音信号了。

在理解耳蜗的运行逻辑后，就可以制造人工耳蜗了。人工耳蜗就是通过手术给耳蜗植入电极，用算法算出声音对应的频率，从而直接刺激相应位置的神经。这样，患者就不仅能感觉到声音，还能分辨声音的高低了。

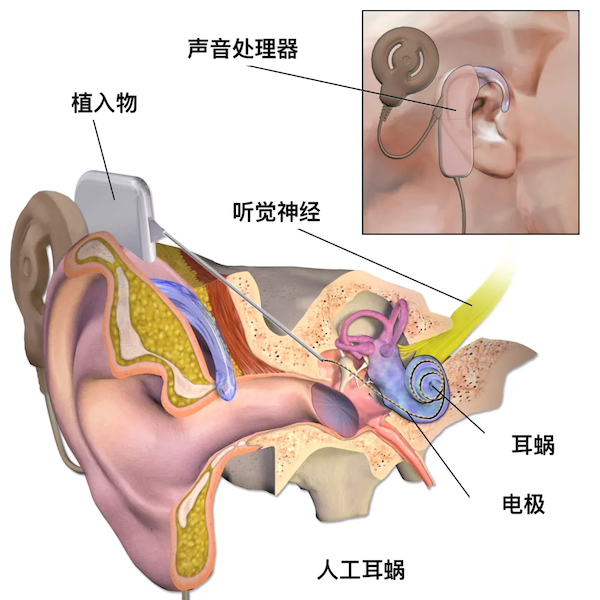
从上世纪70、80年代开始，就陆续有听觉障碍人士植入了人工耳蜗，人工耳蜗的技术也不断随着听力科学的进步而进化。现在，听觉处理器使用的往往不会是单纯的傅立叶变换，从90年代开始，算法逐渐升级成了小波变换，相比短时傅立叶变换更灵活一些。

“超越”数学极限

如果说，人的眼睛本质上只能分辨3种颜色，其他的颜色都是由这3种颜色组合而来，那么我们的耳朵就厉害多了，得益于耳蜗的傅立叶分频设计，我们几乎能连续地分辨从20Hz到20000Hz之间的每一种声音（可能存在个体差异）。但其实，我们耳朵，甚至比数学上单纯的傅立叶变换更厉害一些。

2013年《物理评论快报》（PRL）上的一篇论文指出，人类对声音的频率-时间敏感性，甚至超出了傅立叶变换在数学上的分辨率极限。

你或许听说过量子力学中的测不准原理，就是一个物体的位置和速度（严格来说是动量）不可能同时被完全确定，位置的不确定性和速度的不确定性相乘，有一个最小值。相当于，在量子世界中，如果非常精确的测量一个物体的速度，就不可能确切地知道它的位置，反之亦然。

而量子力学的测不准原理，其实起源于傅立叶变换的数学特征。因为量子力学中使用波函数较多，很多运算操作在数学结构上就相当于傅立叶变换。在量子力学的运算中，从某种程度上来说，一个物体的动量就是它位置的傅立叶变换。物理学家是从傅立叶变换的特征中发现了量子力学的测不准原理。

这个傅立叶变换的特征就是，对原始信号的时间分辨率，和对傅立叶变换后的信号频谱分辨率之间的乘积，存在一个最小值，无论如何也不可能小于1/(4π)。时间分辨率的单位是s，频率分辨率的单位是s⁻¹，二者相乘就是一个没有量纲的数字。

而在这篇论文中，研究人员给受试者随机播放几段时间有限的音频，让他们区分音调的高低。这样，可以通过播放时间限制时间分辨率，通过声音的频率差反映人耳的频率分辨率。结果发现，在几乎每次实验中，受试者的时间-频率分辨率乘积，都小于1/(4π)，有时甚至只有前者的1/10。

当然，这也不是说人类的能力“超越”了数学极限，它反而说明，我们的耳朵其实并非单纯是一个机械的、被动的傅立叶分析装置。傅立叶变换的数学极限只适用于线性结构，我们的耳朵打破了这个极限，就说明我们的耳朵中有一些非线性的增益手段，帮我们不均匀的放大了特定频率、强度的声音。

科学家也并未对这个实验结果感到意外，因为早在1971年，科学家就在动物活体实验中发现了基底膜的非线性特征。目前的猜想是，耳蜗中的外毛细胞充当了这个非线性增益的角色。耳蜗中的毛细胞分为两种，一种名为内毛细胞，它就像我们在上一节中提到的毛细胞一样，能将振动转换成神经信号传入大脑。而另一种毛细胞则是外毛细胞，它能接受来自大脑的信号，主动、不均匀地放大特定频率和强度的声音信号。这种非线性的放大，让人类在对不同频率声音的敏感程度产生了区别。

如果将来有实验能抑制外毛细胞，并且在这种情况下再做一次上述实验，就能验证这种猜想，可惜小编还没有找到有人做这样的实验。

当然，除了外毛细胞，还有一些其他的耳蜗模型在同步探索。再往前，或许就是人类目前认知的边界了。

当你在为傅立叶变换发愁时，你的耳朵甚至已经超越了傅立叶变换，一只脚踏入了非线性的领域。看到这里，你也能明白，初中生物不教听觉原理，确实是有原因的……